L'histoire des réseaux de neurones

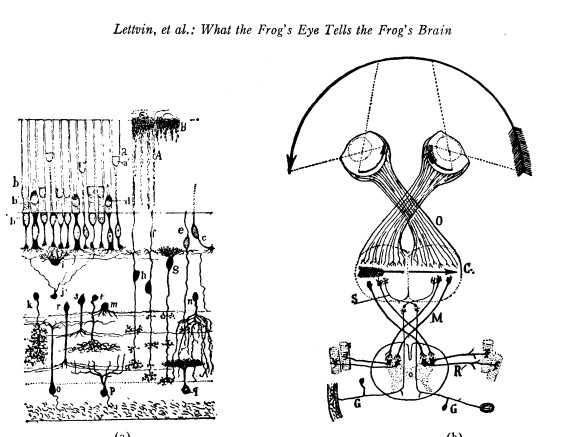
En 1943 deux chercheurs de l’Université de Chicago, le neurophysicien Warren McCullough, et le mathématicien Walter Pitts inventèrent le concept des réseaux de neurones artificiels

Dans un article publié dans le journal Brain Theory, les deux chercheurs présentent leur théorie selon laquelle l’activation de neurones est l’unité de base de l’activité cérébrale.

(Pour aller plus loin, l'un des articles fondateur What the Frog's Eye Tells the Frog's Brain)

Comment fonctionne le réseau de neurones artificiels ?

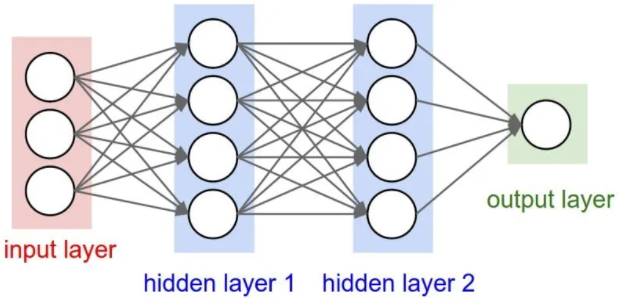
Le cas le plus simple est un réseau de neurones monocouche, donc une seule couhce de neurones cachée

Un réseau de neurones artificels est constitué d'au moins une couche d'entrée, une couche cachée et une couhce de sortie. Chacune comprend un nombre donné de neurones, les neuroens de chaque couche sont connectés aux neurones de la couche suivantes. Les données en entrée activent la couche d'entrée, qui activent à leur tour la couhce suivante et ainsi de suite. On associe un poids à chaque lien (et un biais, on verra ça par la suite). Un algorithme détermine les poids en focntion des données d'apprentissage. Une fois le réseau entrainé suffisament il peut tariter des données du même type que celles sur lesquelles il a étét entrainé

Back Propagation

L'apprentissage Consiste à chercher les meilleurs valeurs de poids pour les meilleurs résultats

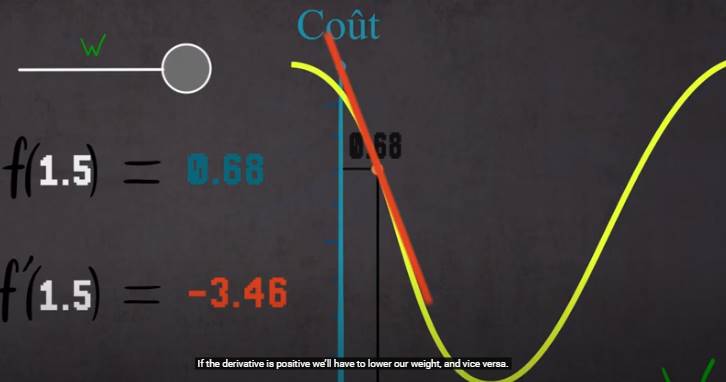
Comment procéder?: Commencer au hasard , propager le signal, à chaque itération comparer le résultat obtenu avec celui attendu = cout (+ élevé si + éloigné) : avec cet indice on sait quel poids a participé à cette erreur : corriger

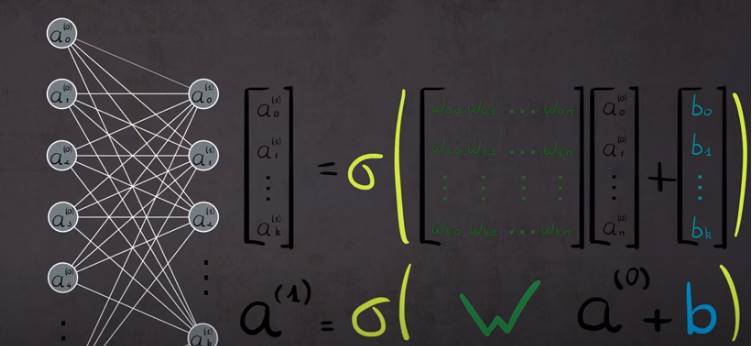
Comment calculer?: Déterminer la fonction d’activationx (Somme entrèes*poids + biais): plusiers fonctions sont utilisées essentiellement la tangente hyperbolique, la sigmoide, rectification linéaire ...

Comment corriger?: Calculer la dérivée (Du poids w), modifié w en fonction pour s’approcher de 0 C’est l’algorithe du gradient (Gradient descent) Procédé de back propagation : corriger les poids qui ont participé à l’erreur) couche par couche en utilisant le gradient descent

Premier RN en python

Prenons un exemple simple où un RN monocouche sera entrainé pour reconnaitre une séquence donnée

Code Source

#Imed 14/06/2021: RN simple 01 en python 
#Reconnaitre la suite 0 1 2 3 en entrée
#le 15/06/2021 ajout d'une seconde couche cachée
#

#import numpy pour la structure des données et les calculs
import numpy as np
np.random.seed(1) #La generation d'aleatoire sera toujours la meme a chaque execution du programme.

#On collectera des données aucours de l'apprentissage 
#Pour viasualiser l'evolution du reseau de neuronne
#import de matplot pour les graphiques et déclaration des variables de stockage des données
import matplotlib.pyplot as plt
xGraphCostFunction=[]
yGraphCostFunction=[]

#Fonction d'activation sigmoide
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

#fonction derivée de notre fonction d'activation
def sigmoidPrime(x):
    return x * (1 - x)


#-------------------   Les données d'entrainement
#Donnes d'inputs
inputs = np.array([ [0, 1, 2, 3],
                    [0, 0, 1, 1],
                    [0, 1, 2, 3],
                    [1, 0, 1, 0],
                    [1, 1, 1, 1]])

#Les donnéed d'outputs (les labels attendus) 
reponses = np.array([[1],
                     [0],
                     [1],
                     [0],
                     [0]])

#Données de vérification. Serviront à vérifier le bon fonctionnement du réseau entrainé 
inputs_test = np.array([[1, 1, 1, 0],
                        [0, 1, 2, 3],
                        [0, 0, 1, 0],
                        [1, 2, 3, 0]])
#----------------------------------------


#------------------   Dimension de notre reseau de neurones
nb_input_neurons = 4        #Nombre de neurones d'entrée
nb_hidden_neurons = 4       #Nombre de neurones dans la couche cachée (Hidden Layer)
nb_hidden2_neurons = 4      #Ime: ajout le 15/06 : On testera avec deux couches cachées pour voir la différence /  Todo ajout d'un biais
nb_output_neurons = 1       #Nombre de neurones de sortie
#------


#Initialisons tout nos poids de manière aleatoire entre -1 et 1
hidden_layer_weights = 2 * np.random.random((nb_input_neurons, nb_hidden_neurons)) - 1
hidden2_layer_weights = 2 * np.random.random((nb_hidden2_neurons, nb_hidden_neurons)) - 1
output_layer_weights = 2 * np.random.random((nb_hidden_neurons, nb_output_neurons)) - 1

print(hidden_layer_weights)
print(hidden2_layer_weights)
print(output_layer_weights)

#===================================
#           Phase d'entrainement
#===================================

#Nombre d'iteration pour la phase d'entrainement
nb_training_iteration = 100000

for i in range(nb_training_iteration):

    #----------------FEED FORWARD-----------------
    # Propage nos informations a travers notre reseau de neurones.

    input_layer = inputs
    hidden_layer = sigmoid(np.dot(input_layer, hidden_layer_weights))   #Fonction de feedforward entre l'input layer et le hidden layer
    hidden2_layer = sigmoid(np.dot(hidden_layer, hidden2_layer_weights))
    output_layer = sigmoid(np.dot(hidden2_layer, output_layer_weights))  #Fonction de feedforward entre le hidden layer et l'ouput layer


    # ----------------BACKPROPAGATION-----------------

    #calcul du cout pour chacune de nos donnes. Represente a quel point on est loin du resultat attendu.
    #L'objectif est de le diminuer le plus possible
    output_layer_error = (reponses - output_layer)
    print("erreur : " + str(output_layer_error))
    # output_layer_error = []

    #Calcul de la valeur avec laquelle on vas corriger nos poids entre le hidden layer et le output layer
    output_layer_delta = output_layer_error * sigmoidPrime(output_layer)

    #Quels sont les poids entre l'input layer et le hidden layer qui ont  contribues a l'erreur, et dans quelle mesure?
    #print("===", output_layer_delta)
    #print("output_layer_weights.T", output_layer_weights.T)
    #print("----", output_layer_weights)
    hidden2_layer_error = np.dot(output_layer_delta, output_layer_weights.T) #.T transposed de 4ligne x1 à 1x4 colonnes


    #Calcul de la valeur avec laquelle on vas corriger nos poids entre le input layer et le hidden layer
    hidden2_layer_delta = hidden2_layer_error * sigmoidPrime(hidden2_layer)

    #propager entre les xdeux couches, re calcul sinon ça    m  rche pas
    hidden_layer_error = np.dot(hidden2_layer_delta,
                                 hidden2_layer_weights.T)  # .T transposed de 4ligne x1 à 1x4 colonnes

    # Calcul de la valeur avec laquelle on vas corriger nos poids entre le input layer et le hidden layer
    hidden_layer_delta = hidden_layer_error * sigmoidPrime(hidden_layer)

    #Correction de nos poids
    output_layer_weights += np.dot(hidden2_layer.T,output_layer_delta)
    hidden2_layer_weights += np.dot(hidden_layer.T, hidden2_layer_delta)
    hidden_layer_weights += np.dot(input_layer.T, hidden_layer_delta)

    #Affichage du cout.
    if (i % 10) == 0:
        cout = str(np.mean(np.abs(output_layer_error))) #Calcul de la moyenne de toute les valeurs de notre erreur
        print("Cout:" + cout)

        #Abscisse du graph -> iteration de la boucle d'apprentissage
        xGraphCostFunction.append(i)
        #Ordonee du grap -> valeure du cout (arrondis a 3 decimales)
        v = float("{0:.3f}".format(float(cout)))
        yGraphCostFunction.append(v)

#===================================
#           Phase de test
#===================================

# Propage nos informations a travers notre reseau de neurones.
input_layer = inputs_test
hidden_layer = sigmoid(np.dot(input_layer, hidden_layer_weights))
output_layer = sigmoid(np.dot(hidden_layer, output_layer_weights))

#Affiche le resultat
print("------")
print("resultat : ")
print(str(output_layer))

#Affiche le graphique
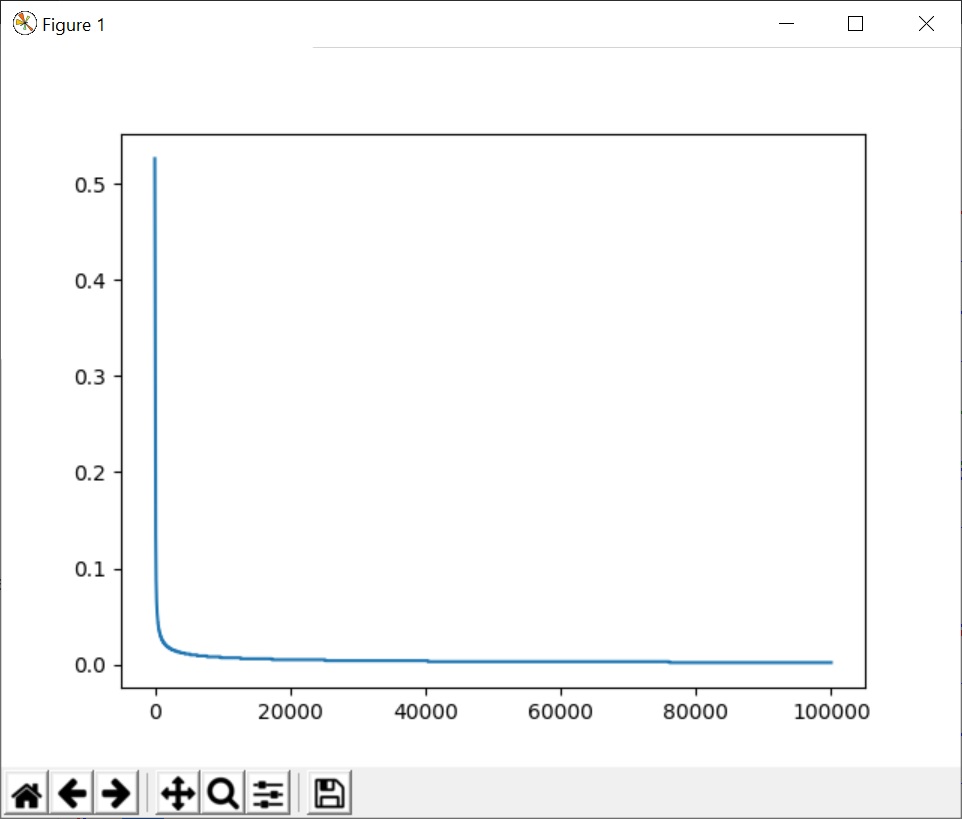
plt.plot(xGraphCostFunction, yGraphCostFunction)
plt.show()

L'affichage du graph de convergence permet de visualiser sa vietees et d'affiner les paramèetres d'apprentissage (fonction d'activiation, irérations .. etc). Nous verrons dans le tutoriel suivant comment l'utilisation des librairies itelles que Tensor Flow KERAS, SciKit Learn peuvent être utilisées pour coder ce même besoin puis pour aller plus loin ...

Le deep learning est une technologie qui se greffe par-dessus de n’importe quelle domaine qui manipule des informations

Les Neural Notworks sont de plus en plus utilisés dans des domaines allant de la reconnaissance d’écriture manuscrite, la transcription ” speech-to-text “, ou encore la prévision des marchés financiers (trading algorithmique), la radio interprétation

D'une manière générale là où il y a des données à traiter surtout dans les cas de reconnaissance de patterns, tatitement des signaux complexes ou la prediction les réseaux de neurones de plus en plus sophistoqués apportent des résulatst dépassanrt parfois la capcaité humaine